Option Greeks – Delta, Theta, Vega, Gamma, Rho

What Are Option Greeks?

The term “Greeks” is used to describe the different dimensions of risk involved in taking an options position. Option Greeks consists of many variables among which delta, theta, gamma, vega, and rho are popular among traders to assess and manage an option’s risk/value/position.

These variables are called Greeks because they are associated with Greek symbols. They are also called as the risk sensitivities, risk measures or hedge parameters. The primary Greeks (Delta, Vega, Theta, Gamma, and Rho) are calculated each as a first partial derivative of the options pricing model.

Basics Of The Option Greeks:

Option Greeks are important to understand as they indicate what factors contribute to the movement in the price of an option and the effect they have. Each of these variables/Greeks has a number associated with it and they change as the price of the stock and time changes. Let’s now understand about the primary option Greeks.

Delta (Δ):

It measures the change in option price in relation to the change in underlying (stock) price, assuming other Greeks remain unchanged.

• Calls have positive delta , between 0 and 1. That means if the stock price goes up and no other pricing variables change, the call option price will also go up. Deep in-the-money (ITM) call option will have a delta of 1, while at-the-money (ATM) call option will have a delta around 0.5 and out-of-the-money (OTM) call option will have a delta of 0.
• Similarly, Puts have negative delta , between 0 and -1. That means if the stock price goes up and no other pricing variables change, the put option price will also go up. Deep in-the-money (ITM) put option will have a delta of -1, while at-the-money (ATM) call option will have a delta around -0.5 and out-of-the-money (OTM) call option will have a delta of 0.
• The ATM option will have 0.5/-0.5 delta because there is 50-50 chance of the option closing in or out-of-the-money at expiration.

Example To Understand Delta:
Assume you have taken a Reliance 1100 call option. If the price of Reliance share is near Rs. 1100 or in other words if your option is at-the-money (ATM) and delta is 0.55 it means you gain Rs 0.55 per share when the share goes up by Rs 1.

The lot size of Reliance is 500 shares, therefore you gain Rs. 275 per lot (500 * 0.55 = 275) when Reliance share moves up by Rs. 1 above 1100.

Gamma (Γ):

Gamma measures the change in Delta with the change in stock price. In other words, gamma represents the rate of change in delta. This is called second-order (second-derivative) price sensitivity. So if delta is the “speed” at which option prices change, you can think of gamma as the “acceleration.”

Options with the highest gamma are the most responsive to changes in the price of the underlying stock. Delta changes as the stock price changes. but it doesn’t change at the same rate for every option based on a given stock.

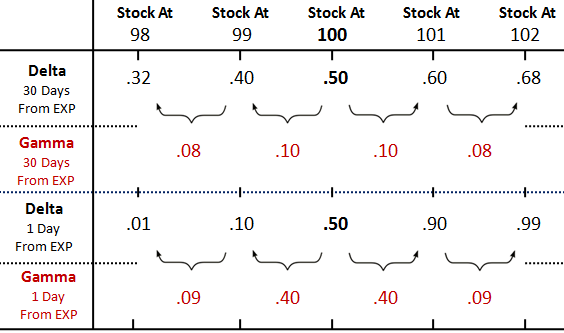
Example: Look at the below image which depicts the change in delta and gamma of the call option of a stock and the strike price chosen is 100, with respect to stock price and time.

Gamma is higher for options that are at-the-money (ATM) and lower for options that are in- and out-of-the-money (ITM & OTM), and accelerates in exponentially as contact expiry date approaches. Higher gamma values indicate that delta could change dramatically in response to even small movements in the underlying’s price.

Theta (Θ):

Theta represents the change in option price as the time to contract expiry decreases, assuming other option Greeks to be constant. It is also known as time sensitivity or option’s time decay or rate of change of the option price with respect to time.

At-the-money options of a stock will experience more significant losses over time than it’s in- or out-of-the-money options.

• In general, time decay or theta is the best friend of the option seller and enemy of the option buyer, as all the OTM options will have no value and all the ATM options will expire with very less premium on expiry. Only ITM or rather deep in-the-money options reward buyers.

Vega (v):

Vega is the change in option price with 1% change in implied volatility (IV), assuming other Greeks are constant. Vega does not have any effect on the intrinsic value of options; it only affects the “time value” of an option’s price.

An increase in implied volatility suggests an increased range of potential movement for the stock. Therefore, as implied volatility increases, the value of options will increase, and decrease in IV will negatively affect the value of options.

Vega is at its maximum for at-the-money (ATM) options that have longer times until expiration. Because, as we go further out in time, there will be more time value built into the option contract. Since implied volatility only affects time value, longer-term options will have a higher Vega than shorter-term options. Vega falls as the option gets closer to expiration.

Rho (p):

Rho represents the change of an option’s value with 1% change in the interest rate.

Except under extreme circumstances, the value of an option is less sensitive to changes in the risk free interest rate than to changes in other parameters. Hence, rho is the least used of the first-order Greeks.

Rho is greatest for at-the-money options with long times until expiration.

• The second and third-order Greeks are hardly used. Therefore, we will discuss about them in some other article. Other than Gamma, the second order Greeks include: Vanna, Charm, Vomma, Veta and Vera.
• The third-order Greeks include: Speed, Zomma, Color and Ultima.